数论魔导--华罗庚
简介
华罗庚(1910年11月12日—1985年6月12日), 原全国政协副主席。出生于江苏常州金坛区,祖籍江苏丹阳,数学家,中国科学院院士,美国国家科学院外籍院士,第三世界科学院院士,联邦德国巴伐利亚科学院院士,中国科学院数学研究所研究员、原所长。
数的一步步扩充
自然数,1、2、3、4、5
负数,-1,出现原因:要减,减不尽
分数,3/2,出现原因:要除,除不尽
以上,总名字,有理数
有理数性质:自封,有理数和有理数进行加减乘除得到的结果还是有理数。有理数 + 有理数 = 有理数,有理数 - 有理数 = 有理数,有理数 × 有理数 = 有理数,有理数 ➗ 有理数(除了0) = 有理数。
无理数,√2,出现原因:勾股定理,边长为 1 的正方形,其对角线长度 √2 并不是有理数。
- 反证法,假设 √2 是有理数,我们记为 √2 = p/q,其中 p 和 q 是没有公约数的
- 那么有 2q² = p²,又因为偶数的平方才可能是偶数,所以 p 为偶数,记为 2p'
- 那么有 q² = 2p'² 所以 q 也必须为偶数
- 这与我们最初假设的 p 和 q 没有公约数的条件是不符合的
- 所以,√2 是无理数
以上,总名字,实数,实数也是自封的。
虚数:a + bi,出现原因:x² + 1 = 0,这个方程无实数根,根只能为虚数,这里是 i,i=√-1。
以上,总名字,复数,复数也是自封的。
域
对 ➕➖✖➗ 自封的数,给它一个定义:域。
面积
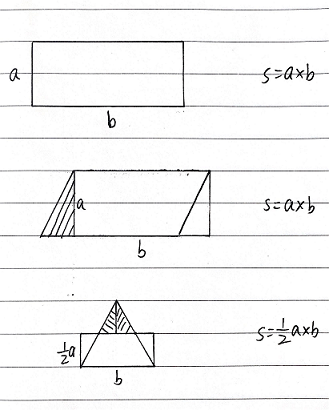
矩形的面积等于长乘以宽,平行四边形可以切割拼接成矩形,三角形也可以切割拼接成矩形。任意多边形都可以切割成三角形求面积。
扩展
数 与 形
连续 与 离散
抽象 与 具体
能行性 与 存在性
必然 与 可能
理论 与 应用
参考:
高等数学第一课